Tree

เรื่อง Tree

เนื้อหา

- โครงสร้างข้อมูลแบบทรี

- นิยามของทรี

- นิยามที่เกี่ยวข้องกับทรี

- การแทนที่ทรีในหน่วยความจำหลัก

- การแปลงทรีทั่วไปให้เป็นไบนารีทรี

- การท่องไปในทรี

- เอกซเพรสชั่นทรี

- ไบนารีเซิร์ชทรี

จุดประสงค์การเรียนรู้

1. เพื่อให้นักศึกษาทราบโครงสร้างข้อมูลแบบทรี

2. เพื่อให้ทราบนิยามของทรี และที่เกี่ยวข้อง

3. เพื่อให้นักศึกษาทราบวิธีการแทนที่ทรีใน หน่วยความจำหลัก

4. เพื่อให้นักศึกษาทราบการแปลงทรีให้เป็นไบ นารีทรี

5. เพื่อให้นักศึกษาทราบวิธีการท่องไปในทรี

6. เพื่อให้นักศึกษาทราบกระบวนการเอกซเพรสชั่นทรี

7. เพื่อให้นักศึกษาทราบวิธีการไบนารีเซิร์ซทรี

ทรี (Tree)ป็นโครงสร้างข้อมูลที่ความสัมพันธ์ ระหว่าง โหนดจะมัความสัมพันธ์ลดหลั่นกันเป็นลำดับ เช่น (Hierarchical Relationship) ได้มีการนำรูปแบบทรีไปประยุกต์ใช้ในงาน ต่าง ๆ อย่างแพร่หลาย สวนมากจะใชสำหรับแสดง ความสัมพันธ์ระหว่างข้อมูล เช่น แผนผังองค์ประกอบของหน่วยงานต่าง ๆ โครงสร้างสารบัญหนังสือ เป็นต้นแต่ละโหนดจะมีความสัมพันธ์กับ โหนดในระดับที่ต่ำลงมา หนึ่งระดับได้หลาย ๆโหนด เรียกโหนดดั้งกล่าวว่า โหนดแม่(Parent orMother Node)โหนดที่อยู่ต่ำกว่าโหนดแม่อยู่หนึ่งระดับเรียกว่า โหนดลูก (Child or Son Node)โหนดที่อยู่ในระดับสูงสุดและไม่มีโหนดแม่เรียกว่า โหดราก (Root Node) Data Structure โหนดที่มีโหนดแม่เป็นโหนดเดียวกัน รียกว่า โหนดพี่น้อง (Siblings)โหนดที่ไม่มีโหนดลูก เรียกว่า โหนดใบ (Leave Node)เส้นเชื่อมแสดงความสัมพันธ์ระหว่าง โหนดสองโหนดเรียกว่า กิ่ง (Branch)

นิยามของทรี1. นิยามทรีด้วยนิยามของกราฟ ทรี คือ กราฟที่ต่อเนื่องโดยไม่มีวงจรปิด (loop)ในโครงสร้าง โหนดสองโหนด ใดๆในทรีต้องมีทางตัดต่อกันทางเดียวเท่านั้น และทรีที่มี N โหนด ต้องมีกิ่ง ทั้งหมด N-1 เส้น การเขียนรูปแบบทรี อาจเขียนได้ 4

2. นิยามทรีด้วยรูปแบบรีเคอร์ซีฟทรีประกอบด้วยสมาชิกที่เรียกว่าโหนด โดยที่ ถ้าว่าง ไม่มีโหนดใด ๆ เรียกว่า นัลทรี (Null Tree)และถามโหนดหนึ่งเป็นโหดราก ส่วนที่เหลือจะแบ่งเป็น ทรีย่อย (Sub Tree)T1, T2, T3,…,Tk โดยที่ k>=0 และทรีย่อยต้องมีคุณสมบัติเป็นทรี

นิยามที่เกี่ยวข้องกับทรี1.ฟอร์เรสต์ (Forest) หมายถึง กลุ่มของทรีที่เกิดจากการเอาโหนดรากของทรีออกหรือเซตของทรีทแยกจากกัน (Disjoint Trees)

2.ทรีที่มีแบบแผน (Ordered Tree) หมายถึง ทรีที่โหนดต่าง ๆ ในทรีนั้นมี ความสัมพันธ์ที่แน่นอน เช่น ไปทางขวาไปทางซ้าย เป็นต้น

3.ทรีคล้าย (Similar Tree) คือทรีที่มีโครงสร้างเหมือนกันหรือทรีที่มีรูปร่างของทรีเหมือนกันโดยไม่คำนึงถึงข้อมูลที่อยู่ในแต่ละโหนด

4.ทรีเหมือน (Equivalent Tree) คือ ทรีที่เหมือนกันโดยสมบูรณ์โดยต้องเป็นทรีที่คล้ายกันและแต่ละโหนดในตำแหน่งเดียวกันมีข้อมูลเหมือนกัน

5.กำลัง (Degree) หมายถึงจำนวนทรีย่อยของโหนด นั้น ๆ เช่น

ในรูปโหนด “B” มีกำลังเป็น 1 เพราะมีทรีย่อย คือ {“D”}ส่วนโหนด “C” มีค่ากำลังเป็นสองเพราะมีทรีย่อย คือ {“E”, “G”, “H”, “I”} และ {“F”}

6.ระดับของโหนด (Level of Node) คือ ระยะทางในแนวดิ่งของโหนดนั้น ๆ ที่อยู่ห่างจากโหนดราก เมื่อกำหนดให้ โหนดรากของทรีนั้นอยู่ระดับ 1 และกิ่งแต่ละกิ่งมีความเท่ากันหมด คือ ยาวเท่ากับ 1หน่วยซึ่งระดับของโหนดจะเท่ากับจำนวนกิ่งที่น้อยที่สุดจากโหนดรากไปยังโหนดใด ๆ บวกด้วย 1และจำนวนเส้นทางตามแนวดิ่งของโหนดใด ๆ ซึ่งห่างจากโหนดราก เรียกวา ความสูง (Height)หรือความ ลึก (Depth)

การแทนที่ทรีในหน่วยความจำหลัก
การแทนที่โครงสร้างข้อมูลแบบทรีในความจำหลักจะมีพอยเตอร์เชื่อมโยงจากโหนดแม่ไปยังโหนดลูก แต่ละโหนดต้องมีลิงค์ฟิลด์เพื่อเก็บที่อยู่ของโหนดลูกต่าง ๆ นั้นคือจำนวน ลิงคฟิลด์ของแต่ละโหนดขึ้นอยู่กับจำนวนของโหนดลูกการแทนที่ทรี ซึ่งแต่ละโหนดมีจำนวนลิงค์ฟิลด์ไม่เท่ากันทำให้ยากต่อการปฏิบัติการ วิธีการแทนที่ที่ง่ายที่สุดคือ ทำให้แต่ละโหนดมีจำนวนลิงคฟิลด์เท่ากันโดยอาจใช่วิธีการต่อไปนี้

1.โหนดแต่ละโหนดเก็บพอยเตอร์ชี้ไปยังโหนดลูก ทุกโหนด การแทนที่ทรีด้วยวิธีนี้จะให้จำนวนฟิลด์ในแต่ละ โหนดเท่ากันโดยกำหนดใหม่ขนาดเท่ากับจำนวนโหนดลูกของโหนดที่มีลูกมากที่สุด โหนดใดไม่มีโหลดลูกก็ให้ค่า พอยเตอร์ในลิงค์ฟิลด์นั้นมีค่าเป็น Null และให้ลิงค์ฟิลด์แรกเก็บค่าพอยเตอร์ชี้ไปยังโหนด ลูกลำดับ ที่หนึ่ง ลิงค์ฟิลด์ที่สองเก็บค่าพอยเตอร์ชี้ไปยังโหนดลูก ลำดับที่สองและลิงค์ฟิลด์อื่นเก็บค่าพอยเตอร์ของโหนดลูก ลำดับถัดไปเรื่อย ๆ

การแทนทรีด้วยโหนดขนาดเท่ากันค่อนข้างใช้เนื้อที่จำนวนมากเนื่องจากแต่ละโหนดมี จำนวนโหนดลูกไม่เท่ากันหรือบางโหนดไม่มี โหนดลูกเลยถ้าเป็นทรีที่แต่ละโหนดมีจำนวนโหนดลูกที่แตกต่างกันมากจะเป็นการสิ้นเปลือง เนื้อที่ในหน่วยความจำโดยเปล่าประโยชน์

2.แทนทรีด้วยไบนารีทรีเป็นวิธีแก้ปัญหาเพื่อลดการ สิ้นเปลืองเนื้อที่ในหน่วยความจำก็คือ กำหนดลิงค์ฟิลด์ใหม่จำนวนน้อยที่สุดเท่าที่จำเป็นเท่านั้นโดยกำหนดให้แต่ละโหนดมีจำนวนลิงค์ฟิลด์สองลิงค์ฟิลด์-ลิงค์ฟิลด์แรกเก็บที่อยู่ของโหนดลูกคนโต-ลิงค์ฟิลด์ทสองเก็บที่อยู่ของโหนดพี่น้องที่เป็นโหนดถัดไปโหนดใดไม่มีโหนดลูกหรือไม่มีโหนดพี่น้องให้ค่าพอยนเตอร์ใน ลิงค์ฟิลด์มีค่าเป็น Null

โครงสร้างทรีที่แต่ละโหนดมีลิงค์ฟิลด์แค่สองลิงค์ฟิลด์ ซึ่งช่วยให้ประหยัดเนื้อที่ในการจัดเก็บได้มาก เรียกโครงสร้างทรีที่แต่ละโหนดมีจำนวนโหนดลูกไม่เกินสองหรือแต่ละโหนดมีจำนวน ทรีย่อยไม่เกินสองนี้ว่า ไบนารีทรี (Binary Tree)

ไบนารีทรีที่ทุก ๆ โหนดมีทรีย่อยทางซ้ายและทรีย่อยทางขวา ยกเว้นโหนดใบ และโหนดใบทุกโหนดจะต้องอยู่ที่ระดับเดียวกันเรียกว่า ไบนารีทรีแบบสมบูรณ์ (complete binary tree)สามารถคำนวณจำนวนโหนดทั้งหมดในไบนารีทรีแบบสมบูรณ์ได้ถ้ากำหนดให้ Lคือระดับของโหนดใด ๆ และ N คือจำนวนโหนดทั้งหมดในทรีจะได้ว่า
ระดับ 1 มีจำนวนโหนด 1 โหนด
ระดับ 2 มีจำนวนโหนด 3 โหนด
ระดับ 3 มีจำนวนโหนด 7 โหนด
ระดับ L มีจำนวนโหนด 2L - 1โหนด
นั้นคือ จำนวนโหนดทั้งหมดในทรีสมบูรณ์ที่ มี L ระดับ สามารถคำนวณได้จากสูตรดั้งนี้

การแปลงทรีทั่วไปให้เป็นไบนารีทรี
ขั้นตอนการแปลงทรีทั่วๆ ไปให้เป็นไบนารีทรี มีลำดับขั้นตอนการแปลง ดั้งต่อไปนี้
1. ให้โหนดแม่ชี้ไปยังโหนดลูกคนโต แล้วลบความสัมพันธ์ ระหว่างโหนดแม่และโหนดลูกอื่น ๆ
2. ให้เชื่อมความสัมพันธ์ระหว่างโหนดพี่น้อง
3. จบให้ทรีย่อยทางขวาเอียงลงมา 45 องศา

การท่องไปในไบนารีทรี
ปฏิบัติการที่สำคัญในไบนารีทรี คือ การท่องไปในไบนารีทรี (Traversing Binary Tree) เพื่อเข้าไปเยือนทุก ๆโหนดในทรี ซึ่งวิธีการท่องเข้าไปต้องเป็นไปอย่างมีระบบแบบแผน สามารถเยือนโหนดทุก ๆโหนด ๆ ละหนึ่งครั้งวิธีการท่องไปนั้นมีด้วยกันหลายแบบแล้วแต่ว่าต้องการลำดับขั้นตอนการเยือนอย่างไร โหนดที่ถูกเยือนอาจเป็นโหนดแม่ (แทนด้วย N)ทรีย่อยทางซ้าย (แทนด้วย L)หรือทรีย่อยทางขวา (แทนด้วย R)

มีวิธีการท่องเข้าไปในทรี 6 วิธี คือ NLR LNR LRN NRL RNL และ RLN แต่วิธีการท่องเข้าไปไบนารีทรีที่นิยมใช้กันมากเป็นการท่องจากซ้ายไปขวา 3 แบบแรกเท่านั้นคือ NLR LNR และ LRN ซึ่งลักษณะการนิยามเป็นนิยามแบบ รีเคอร์ซีฟ(Recursive) ซึ่งขั้นตอนการท่องไปในแต่ละแบบมีดังนี้
1. การท่องไปแบบพรีออร์เดอร์(Preorder Traversal) เป็นการเดินเข้าไปเยือนโหนดต่าง ๆ ในทรีด้วยวิธีNLR มีขั้นตอนการเดินดังต่อไปนี้
(1) เยือนโหนดราก
(2) ท่องไปในทรีย่อยทางซ้ายแบบพรีออร์เดอร์
(3) ท่องไปในทรีย่อยทางขวาแบบพรีออร์เดอร์

2.การท่องไปแบบอินออร์เดอร์(Inorder Traversal)เป็นการเดินเข้าไปเยือนโหนดต่าง ๆในทรีด้วยวิธี LNRมีขั้นตอนการเดินดังต่อไปนี้
(1) ท่องไปในทรีย่อยทางซ้ายแบบอินออร์เดอร์
(2) เยือนโหนดราก
(3) ท่องไปในทรีย่อยทางขวาแบบอินออร์เดอร์

3. การท่องไปแบบโพสออร์เดอร์(Postorder Traversal)เป็นการเดินเข้าไปเยือนโหนดต่าง ๆในทรีด้วยวิธี LRN มีขั้นตอนการเดินดังต่อไปนี้
(1) ท่องไปในทรีย่อยทางซ้ายแบบโพสต์ออร์เดอร์
(2) ท่องไปในทรีย่อยทางขวาแบบโพสต์ออร์เดอร์

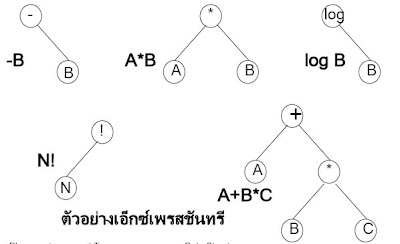
เอ็กซ์เพรสชันทรี (Expression Tree)
เป็นการนำเอาโครงสร้างทรีไปใช้เก็บนิพจน์ทางคณิตศาสตร์โดยเป็นไบนารีทรี ซึ่งแต่ละโหนดเก็บตัวดำเนินการ (Operator) และและตัวถูกดำเนินการ(Operand) ของนิพจน์คณิตศาสตร์นั้น ๆ ไว้ หรืออาจจะเก็บค่านิพจน์ทางตรรกะ (Logical Expression)นิพจน์เหล่านี้เมื่อแทนในทรีต้องคำนึงลำดับขั้นตอนในการคำนวณตามความสำคัญของเครื่องหมายด้วยโดยมีความสำคัญตามลำดับดังนี้

- ฟังก์ชัน
- วงเล็บ
- ยกกำลัง
- เครื่องหมายหน้าเลขจำนวน (unary)
- คูณ หรือ หาร
- บวก หรือ ลบ
- ถ้ามีเครื่องหมายที่ระดับเดียวกันให้ทำจากซ้ายไปขวา
การแทนนิพจน์ในเอ็กซ์เพรสชันทรี ตัวถูกดำเนินการจะเก็บอยู่ที่โหนดใบส่วนตัวดำเนินการจะเก็บในโหนดกิ่งหรือโหนดที่ไม่ใช่โหนดใบเช่น นิพจน์ A + B สามารถแทนในเอ็กซ์เพรสชันทรีได้ดังนี้

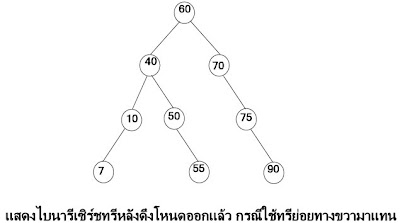
ไบนารีเซิร์ชทรี
ไบนารีเซิร์ชทรี (Binary Search Tree)เป็นไบนารีทรีที่มีคุณสมบัติที่ว่าทุก ๆ โหนดในทรี ค่าของโหนดรากมีค่ามากกว่าค่าของทุกโหนดในทรีย่อยทางซ้าย และมีค่าน้อยกว่าหรือเท่ากับค่าของทุกโหนดในทรีย่อยทางขวาและในแต่ละทรีย่อยก็มี คุณสมบัติเช่นเดียวกัน

ปฏิบัติการในไบนารีเซิร์ชทรี ปฏิบัติการเพิ่มโหนดเข้าหรือดึงโหนดออกจากไบนารีเซิร์ชทรีค่อนข้างยุ่งยากกว่าปฏิบัติการในโครงสร้างอื่น ๆเนื่องจากหลังปฏิบัติการเสร็จเรียบร้อยแล้วต้องคำนึงถึงความเป็นไบนารีเซิร์ชทรีของทรีนั้นด้วยซึ่งมีปฏิบัติการดังต่อไปนี้

(1) การเพิ่มโหนดในไบนารีเซิร์ชทรี การเพิ่มโหนดใหม่เข้าไปในไบนารีเซิร์ชทรี ถ้าทรีว่างโหนดที่เพิ่มเข้าไปก็จะเป็นโหนดรากของทรี ถ้าทรีไม่ว่างต้องทำการตรวจสอบว่าโหนดใหม่ที่เพิ่มเข้ามานั้นมีค่ามากกว่าหรือน้อยกว่าค่าที่โหนดราก ถ้ามีค่ามากกว่าหรือเท่ากันจะนำโหนดใหม่ไปเพิ่มในทรีย่อยทางขวาและถ้ามีค่าน้อยกว่านำโหนดใหม่ไปเพิ่มในทรีย่อยทางซ้ายในทรีย่อยนั้นต้องทำการเปรียบเทียบในลักษณะเดียวกันจนกระทั่งหาตำแหน่งที่สามารถเพิ่มโหนดได้ ซึ่งโหนดใหม่ที่

(2) การดึงโหนดในไบนารีเซิร์ชทรีหลังจากดึงโหนดที่ต้องการออกจากทรีแล้วทรีนั้นต้องคงสภาพไบนารีเซิร์ชทรีเหมือนเดิมก่อนที่จะทำการดึงโหนดใด ๆ ออกจากไบนารีเซิร์ชทรี ต้องค้นหาก่อนว่าโหนดที่ต้องการดึงออกอยู่ที่ตำแหน่งไหนภายในทรีและต้องทราบที่อยู่ของโหนดแม่โหนดนั้นด้วยแล้วจึงทำการดึงโหนดออกจากทรีได้ ขั้นตอนวิธีดึงโหนดออกอาจแยกพิจารณาได้ 3กรณีดังต่อไปนี้

ก. กรณีโหนดที่จะดึงออกเป็นโหนดใบการดึงโหนดใบออกในกรณีนี้ทำได้ง่ายที่สุดโดยการดึงโหนดนั้นออกได้ทันที เนื่องจากไม่กระทบกับโหนดอื่นมากนัก วิธีการก็คือให้ค่าในลิงค์ฟิลด์ของโหนดแม่ซึ่งเก็บที่อยู่ของโหนดที่ต้องการดึงออกให้มีค่าเป็น Null

ข. กรณีโหนดที่ดึงออกมีเฉพาะทรีย่อยทางซ้ายหรือทรีย่อยทางขวาเพียงด้านใดด้านหนึ่ง วิธีการดึงโหนดนี้ออกสามารถใช้วิธีการเดียวกับการดึงโหนดออกจากลิงค์ลิสต์ โดยให้โหนดแม่ของโหนดที่จะดึงออกชี้ไปยังโหนดลูกของโหนดนั้นแทน

ค. กรณีโหนดที่ดึงออกมีทั้งทรีย่อยทางซ้ายและทรีย่อยทางขวาต้องเลือกโหนดมาแทนโหนดที่ถูกดึงออก โดยอาจจะเลือกมาจากทรีย่อยทางซ้ายหรือทรีย่อยทางขวาก็ได้
- ถ้าโหนดที่มาแทนที่เป็นโหนดที่เลือกจากทรีย่อยทางซ้ายต้องเลือกโหนดที่มีค่ามากที่สุดในทรีย่อยทางซ้ายนั้น
- ถ้าโหนดที่จะมาแทนที่เป็นโหนดที่เลือกมาจากทรีย่อยทางขวา ต้องเลือกโหนดที่มีค่าน้อยที่สุดในทรีย่อยทางขวานั้น

 จงเลือกคำตอบที่ถูกต้องเพียงคำตอบเดียว โดยทำเครื่องหมาย X ทับตัวเลือกที่ต้องการ

1.โครงสร้างข้อมูลแบบต้นไม้เป็นโครงสร้างชนิดใด

  ก. ชนิดเชิงเส้น

  ข. ชนิดไม่เชิงเส้น

  ค. ชนิดตัดสินใจเลือก

  ง. ชนิดทำงานซ้ำ

2. โหนดพิเศษโหนดหนึ่งที่อยู่บนสุดแรกเรียกว่าอะไร

  ก. Father

  ข. Subtree

  ค. Leat Node

  ง. Root Node

3. Level มีความหมายตรงกับข้อใด

  ก. รูท

  ข. ดีกรีของโหนด

  ค. โหนดที่เป็นใบ

  ง. ระดับของโหนด

4. ดีกรีของโหนดคืออะไร

  ก. รูทโหนด

  ข. จำนวนต้นไม้ 1 ต้น

  ค. ต้นไม้แบบพรีออเดอร์

  ง. จำนวนต้นไม้ย่อยของโหนดนั้น

5. ป่าไม้ในโครงสร้างข้อมูลแบบต้นไม้ หมายถึงสิ่งใด

  ก. กลุ่มของต้นไม้

  ข. ต้นไม้ย่อยซ้าย

  ค. ต้นไม้ย่อยขวา

  ง. การดูแลต้นไม้

6. โครงสร้างข้อมูลแบบต้นไม้ มีลักษณะคล้ายสิ่งใด

  ก. ใบไม้

  ข. รากของต้นไม้

  ค. ลำต้นของต้นไม้

  ง. กิ่งก้านของต้นไม้

7. ต้นไม้ธรรมชาติจะงอกจากล่างขึ้นบน ส่วนโครงสร้างข้อมูลแบบต้นไม้นั้นจะเจริญเติบโตอย่างไร

  ก.จากล่างไปบน

  ข. จากบนลงล่าง

  ค. จากซ้ายไปขวา

  ง. จากขวาไปซ้าย

8. ต้นไม้ Binary ที่แต่ละโหนดภายในจะมีโหนดย่อยซ้ายโหนดย่อยขวาและโหนดใบหมายถึงต้นไม้แบบใด

  ก. ต้นไม้ไบนารีคู่

  ข. ต้นไม้ไบนารีเดี่ยว

  ค. ต้นไม้ไบนารีแบบสมบูรณ์

  ง. ต้นไม้ไบนารีแบบไม่สมบูรณ์

9. ข้อใดไม่ใช่การแทนต้นไม้ไบนารีในหน่วยความจำ

  ก. การแทนโดยอาศัยพอยน์เตอร์

  ข การแทนโดยอาศัยแอดเดรสของโหนด

  ค. การแทนแบบวีแควนเชียล

  ง. การแทนแบบลำดับชั้น

10. LVR คือวิธีการเดินเข้าแบบใด

  ก. แบบพรีออร์เดอร์

  ข. แบบอินออร์เดอร์

  ค. แบบโพสต์ออร์เดอร์

  ง. ไม่มีข้อใดถูก

เฉลย  1.ข 2.ง 3.ง 4.ง 5.ก 6.ง 7.ข 8.ค 9.ง 10.ข

ข้อมูลสแตก

โครงสร้างข้อมูลสแตก

โครงสร้างสแตก

โครงสร้างสแตกข้อมูลที่รู้จักและนำมาใช้งานชนิดหนึ่งก็คือ สแตก (Stack) มีลักษณะเป็นรายการในแนวเชิงเส้น(Linear List) รูปแบบหนึ่ง และมีข้อกำหนดให้ชุดปฏิบัติการ สามารถเพิ่มและลบรายการเพียงด้านเดียว ซึ่งเป็นด้านบนสุดของสแตก (Top of Stack)เรียกว่าตัวชี้สแตก (Stack Pointer) มีรูปแบบเป็น (Top)(S)โดยสแตกมีการกำหนดเป็นรูปแบบดังนี้S = [s1 ,S2, … ,ST]ด้านบนสุดของสแตกจะอยู่ที่ Top (S) =ST และมีจำนวนสมาชิกในสแตกเท่ากับ T

ดังในรูปที่ 4.1

ST

…

S2

S1

รูปที่ 4.1 ตัวอย่างลักษณะสแตกที่มีสมาชิกเท่ากับ T มีตัวชี้สแตก Top

ปัญหาที่ 1  เนื่องจากคอมพิวเตอร์ทำงานในรูปแบบของเลขฐาน 2 แต่ในส่วนของผู้ใช้งานจะเป็นเลขฐาน 10 จึงต้องแปลงค่าจากเลขฐาน 10 ไปเป็นเลขฐาน 2 เช่น เปลี่ยนจาก 26 เป็น 11010

ปัญหาที่ 2  คอมไพเลอร์ (Compiler) จะต้องคำนวณนิพจน์ (Expression) ทางคณิตศาสตร์ที่มีเครี่องหมายวงเล็บเปิดและปิดเข้ามาเกี่ยวข้อง

ปัญหาที่ 3  โปรแกรมเกมเล่นไพ่ (Card Game) จะมีที่วางกองไพ่และการแจกไพ่ได้เฉพาะใบที่อยู่บนสุด

ปัญหาที่ 4  รูปแบบปัญหาการทำงานบางอย่าง  เช่น  การทำงานของ  Switching Box ของเครือข่าย หรือรูปแบบการสลับตู้รถไฟบนราง  ดังในรูปที่ 4.3

ปัญหาต่าง ๆ  เหล่านี้สามารถแก้ไขโดยใช้โครงสร้างสแตก  ซึ่งมีลักษณะการทำงานในรูปแบบที่เรียกว่าเข้าทีหลังออกก่อน(Last-In-First-Out, LIFO) เมื่อมีค่าใหม่เข้ามาก็จะใส่ลงในสแตกซ้อนทับค่าเดิมที่เก็บอยู่ลงไปอยู่ด้านล่างไปเรื่อย ๆ ในลักษณะแบบนี้

การปฏิบัติการของสแตก

จากลักษณะดังที่กล่างมาของสแตก  จะต้องมีการปฏิบัติการเข้ามาช่วยการทำงานของสแตกให้มีความถูกต้อง

1. CreateStack( ) ใช้สร้างสแตกใหม่ขึ้นมาใช้งานและกำหนดค่าเริ่มต้นต่าง ๆ

2. Push(value,  stack)  ใช้เพิ่มค่าใหม่เก็บลงในสแตกที่ใช้งานอยู่  มีอัลกอริทึมการทำงานเป็นดังในตารางที่ 4.1

ตารางที่ 4.1  อัลกอริทึมการเพิ่มค่าใหม่เก็บลงในสแตก

1.  ตรวจสอบสแตกว่าจะมีสมาชิกอยู่เต็มหรือไม่  โดยเปรียบเทียบค่า Top กับขนาดอาร์เรย์

2.  ถ้าสแตกไม่เต็ม

2.1  เพิ่มค่าให้กับ Top โดยการบวก 1

2.2  ทำการนำค่าที่ได้มาเก็บลงในสแตกในตำแหน่ง Top ไม่เช่นนั้นแจ้งกลับมาว่าสแตกเต็ม

3.  Pop(stack)  ใช้ดึงค่าออกจากสแตกที่ใช้งานอยู่และส่งค่า value กลับมาให้ มีอัลกอริทึมการ   ทำงานเป็นดังในตารางที่ 4.2

 ตารางที่ 4.2  อัลกอริทึมดึงค่าออกจากสแตก

1.    ตรวจสอบว่าสแตกว่างหรือไม่ โดยเปรียบเทียบค่า Top กับขนาดอาร์เรย์

2.    ถ้าสแตกไม่ว่าง

2.1  ทำการดึงค่าในตำแหน่ง  Top ออกมาให้

2.2  ลดค่าของ Top โดยการลบ 1 ไม่เช่นนั้นแจ้งกลับมาว่าสแตกว่าง

3.  isEmpty(stack)  ใช้ตรวจสอบว่าสแตกที่ใช้งานอยู่ว่างหรือไม่  ถ้าไม่มีค่าเก็บไว้เลยจะส่งค่าจริงกลับให้

เมื่อนำสแตกมาใช้งานตามลำดับดังในรูป (a) ถึง (g) มีการทำงานโดยใช้ชุดปฏิบัติการ Push และ Pop ดังนี้

(a)  เริ่มต้นสร้างสแตก  S ขึ้นมาทำงานจะได้เป็นสแตกว่าง  ไม่มีสมาชิกโดยตัวชึ้สแตก Top ยังไม่มีค่า

(b) นำค่า  A  เข้ามาเก็บเป็นตัวแรกโดยใช้  Push(A) สแตก S = [A] ตัวชี้สแตก Top = A

(c) นำค่า  B เก็บต่อโดยใช้ Push(B) สแตก S = [A,B] ตัวชี้สแตก Top = B

(d) นำค่า C เก็บต่อโดยใช้ Push(C) สแตก S = [A,B,C]ตัวชี้สแตก Top =C

(d) ต้องการดึงค่าออกมาโดยใช้ Pop( ) สแตก S = [A,B] ตัวชี้สแตกTop = B

(f) นำค่า D, E เก็บต่อโดยใช้ Push(D) และ Push(E) ตามลำดับ สแตก

S = [A,B,D,E] ตัวชี้สแตก Top = E

(g) ดึงค่าออกมา 3 ค่าโดยใช้ Pop( )  3  ครั้งและเก็บค่า F โดยใช้ Push(F) สแตก S = [A,F] ตัวชี้สแตก Top = F

จะเห็นว่าการทำงานของสแตกเมื่อมีค่าใดส่งเข้ามาเก็บเป็นตัวสุดท้ายก็จะอยู่บนสุด  ค่าที่ใส่ลงมาก่อนหน้านี้ก็จะถูกซ้อนทับตามลำดับ  หากมีการดึงค่าออกมาใช้ค่าที่อยู่บนสุดจะถูกดึงออกมาก่อน  ลักษณะที่ได้จึงเป็นการกลับกันของลำดับการใช้งานและเรียกว่าเข้าทีหลังออกก่อน

ตัวอย่างการใช้สแตก

จากปัญหาในตอนต้นกล่าวถึงปัญหาการเปลี่ยนเลขฐาน  10  เป็นเลขฐาน  2   เนื่องจากการคำนวณเป็นการหารเลขฐาน  10  เศษที่เหลือจะได้เป็นเลขฐาน  2  เมื่อนำมาแสดงผลจะเป็นตัวเลขจากซ้ายไปขวา  แต่เลขฐาน  2  เป็นตัวเลขจากขวาไปซ้ายจึงเกิดการสลับด้านกัน  จึงนำสแตกมาช่วยแก้ปัญหานี้  ดังในตารางที่ 4.3 คือ โปรแกรม Stack.c

เป็นการสร้างสแตกขึ้นมาโดยใช้โครงสร้างข้อมูลเรคคอร์ด   และสร้างชุดปฏิบัติการให้กับสแตกขึ้นมาสำหนับเรียกใช้งานเพื่อแก้ใขการเปลี่ยนเลขฐาน  10  เป็นเลขฐาน  2  จากค่าที่ได้รับเข้าทางคีย์บอร์ด  สแตกทีได้เป็นแบบไดนามิกคือขอใช้พื้นที่หน่วยความจำให้กับสแตกตอนที่โปรแกรมทำงาน  ทำให้มีสแตกได้หลายตัวมาใช้งานพร้อมกันโดยที่ใช้ชุดปฏิบัติการเดียวกันจากตัวอย่างจะใช้สแตกเพียวตัวเดียว

การใช้สแตกแก้ปัญหาการแปลงนิพจน์คณิตศาสตร์

คอมไพเลอร์จะแปลงคำสั่งจากภาษาระดับสูง  (High-level  Language)  ไปเป็นภาษาเครื่อง(Machine Language) ส่วนหนึ่งที่ต้องแปลงคือนิพจน์คณิตศาสตร์ เช่น X = A * B + C ซึ่งมีลักษณะที่เรียกว่า  Infix  Notation  มีเครื่องหมายคำนวณอยู่ระหว่างโอเปอแร้น (Operand) โดยแปลงไปเป็นนิพจน์แบบPostfix  Notation มีเครื่องหมายคำนวณนำหน้าโอเปอแร้น แต่เนื่องจากนิพจน์แบบ Infix มีการนำเครื่องหมายวงเล็บเข้ามาใช้ทำให้ทิศทางการคำนวณเปลี่ยนไป   ดังในตารางที่ 4.4 เป็นตัวอย่างของการคำนวณแบบเดียวกัน

ตารางที่ 4.4  ลักษณะนิพจน์แบบ Infix,Postfix, และ Prefix Notation

Infix	Postfix	Prefix
A+(B*C)

(A+B)*C

A+B-C

(A+B)*(C-D)

(A+B)*C-(D-E) ) $ (F+G)ABC*+

AB+C*

AB+C-

AB+CD-*

AB+C*DE—FG+$+A*BC

*+ABC

-+ABC

*+AB-CD

$-*+ABC-DE+FG

การแปลงนิพจน์แบบ Infix เป็นแบบ Postfix

เมื่อพิจารณาการแปลงนิพจน์แบบ Infix เป็นแบบPostfixเป็นขั้นตอนการแปลงโดยเริ่มต้นจากสแกนนิพจน์Infix ทีละตัว  หากพบวงเล็บก็จะทำส่วนที่อยู่ในวงเล็บให้เสร็จก่อนเป็นนิพจน์ย่อย (Subexpression) ซึ่งจะได้เป็นอัลกอริทึมดังในตารางที่ 4.5

 ตารางที่ 4.5  อัลกอริทึมการแปลงนิพจน์แบบ Infix เป็นแบบ Postfix

1. สร้างสแตกที่ว่างเปล่ายังไม่มีการเก็บค่า
2. ถ้าค่าในนิพจน์ Infix ยังไม่หมด หรือเกิดข้อผิดพลาด ให้ทำดังนี้
3. a.  รับค่า  (Token) ตัวถัดไปในนิพจน์  Infix (ประกอบด้วย ค่าคงที่ ตัวแปร เครื่องหมายคำนวณ วงเล็บเปิดและปิด
4. b. ค่าที่รับเข้ามา ถ้าเป็น
5. b.1  โอเปอแร้น (ค่คงที่,ตัวแปร)นำไปแสดงทางจอภาพ
6. b.2  วงเล็บเปิดนำใส่ลงในสแตก (Push)
7. b.3  วงเล็บปิด ดึงค่าออกจากสแตก (Pop) และนำไปแสดงทางจอภาพ  ทำจนกว่าจะพบวงเล็บเปิด
8. b.4  เครื่องหมายคำนวน ถ้าสแตกว่าง  หรือค่าที่รับมามี Precedence สูงกว่าค่าบนสแตกให้นำใส่ลงในสแตก (Push) ถ้าหากค่าที่รับมามี Precedence น้อยกว่าค่าบนสแตกให้ดึงค่าออกจากสแตก (Pop)
9. เมื่อทำจนค่าในนิพจน์ Infix หมด ให้ดึงค่าออกจากสแตก (Pop) แสดงทางจอภาพตามลำดับ จนกว่าสแตกว่าง

ตารางที่ 4.6 การแปลงนิพจน์ 7*8-(2+3) เป็นนิพจน์ Postfixจากอัลกอริทึมดังกล่าวเมื่อนำมาใช้กับตัวอย่างนิพจน์ 7*8-(2+3) จะได้เป็นลำดับขั้นตอนดังในรูปที่ 4.4 หรือเขียนเป็นแบบตารางได้ดังในตารางที่ 4.6

นิพจน์ Infix	สแตก	นิพจน์ Postfix
7*8-(2+3)

*8-(2+3)

8-(2+3)

-(2+3)

(2+3)

2+3)

+3)

3)

) 

*

–

– (

–         ( +

-7

7 8

7 8 *

7 8 *2

7 8 *2 3

/ 8 *2 3 +

7 8 * 2 3 + –

การหาค่าคำตอบจากการคำนวณนิพจน์ Postfix

จากการแปลงนิพจน์แบบ Infix เป็นแบบ Postfix ทำให้นิพจน์ที่ได้ไม่มีเครื่องหมายวงเล็บ  ต่อจากนั้นจะทำการหาค่าคำตอบโดยสแกนนิพจน์ Postfix ทีละตัวจากซ้ายไปขวา เมื่อใดที่พบโอเปอแร้นก็นำเก็บลงในสแตก  สุดท้ายคำตอบที่ได้จะอยู่ในสแตกเพียงค่าเดียวซึ่งจะได้เป็นอัลกอริทึมดังในตารางที่ 4.7

ตารางที่ 4.7  อัลกอริทึมการหาค่าคำตอบจากนิพจน์ Postfix

1.     สร้างสแตกที่ว่างเปล่ายังไม่มีการเก็บค่า

2.ทำงานต่อไปนี้ซ้ำจนกว่าถึงจุดสิ้นสุดของนิพจน์a. รับค่า (Token) ตัวถัดไปในนิพจน์ RPN (ประกอยด้วย  ค่าคงที่  ตัวแปร  เครื่องหมายคำนวณ)

b  ค่าที่รับเข้ามา  ถ้าเป็นโอเปอแร้น ให้นำใส่ลงในสแตก (Push) แต่ถ้าเป็นเครื่องหมายคำนวณให้ทำดังนี้

b.1  ดึงค่าออกจากสแตก (Pop) สองค่า ถ้าไม่ครบให้แจ้งเกิดข้อผิดพลาด

b.2  นำเครื่องหมายคำนวณทำการประมวลผลกับค่าทั้งสอง

b.3  นำผลลัพธ์ที่ได้ใส่กลับลงในสแตก (Push)

3.  เมื่อถึงจุดสิ้นสุดของนิพจน์ ค่าที่เป็นคำตอบจะอยู่บนสแตก ซึ่งมีเพียงค่าเดียวเท่านั้น

จากอัลกอริทึมดังกล่างเมื่อนำมาใช้กับตัวอย่างนิพจน์ 2 4 *9 5 + -จะเป็นตามลำดับขั้นตอนดังในรูปที่ 4.5 หรือเขียนเป็ฯแบบตารางได้ดังในตารางที่ 4.8

ตารางที่ 4.8 การหาค่าคำตอบจากนิพจน์

นิพจน์ Postfix	ค่าที่ได้	สแตก
2 4 * 9 5 + –

4 + 9 5 + –

* 9 5 + –

9 5 + –

5 + –

+ –

– 

2 * 4 = 8

9 + 5 = 14

8 – 14 = -62

2 4

8

8 9

8 9 5

8 14

-6

-6

ตอนที่ 1 จงเลือกคำตอบที่ถูกต้องเพียงคำตอบเดียว โดยทำเครื่องหมาย X ทับตัวเลือกที่ต้องการ

1.การนำข้อมูลเข้าสแต็กเรียกว่าอะไร

  ก. Push

  ข. Pop

  ค. Stack

  ง. Top

2. คุณสมบัติของสแต็กที่เรียกว่า LIFO เนื่องจากสาเหตุใด

  ก. มีบัฟเฟอร์สำรองและจัดสรรการเข้าออกของข้อมูล

  ข. ข้อมูลเข้าก่อนออกก่อนข้อมูลเข้าทีหลัง ออกทีหลัง

  ค. ข้อมูลเข้าก่อนออกทีหลัง ข้อมูลเข้าที่หลังออกก่อน

  ง. ข้อมูลเข้าก่อนมีสิทธิออกก่อน หรือทีหลังก็ได้

3. ข้อใดที่กล่าวถึง Operations เกี่ยวกับสแต็กไม่ถูกต้อง

  ก. Push A

  ข. Push 20

  ค. Pop A

  ง. Pop

4. ขณะที่สแต็กว่าง ถ้ามีการดำเนินการ Push W , Push D , Push x , Push Q , หลังจากนั้นทำการ Pop ค่าที่ออกจากแสต็กคือค่าใดบ้าง

  ก. W    D     X       Q

  ข. W    D     Q       X

  ค. Q     X     D      W

  ง. Q     X     W     D

5. ข้อใดที่เป็นนิพจน์อินฟิกซ์

  ก. A+B-C

  ข. +AB-C

  ค. +-ABC

  ง. AB+C-

6. ข้อใดที่เป็นนิพจน์โฟสต์ฟิกซ์

  ก. A+B-C

  ข. +AB-C

  ค. +-ABC

  ง. AB+C-

7. ข้อใดเป็น Operators ทั้งหมด

  ก. +   -   *   /    ^

  ข. +  ( )    =   >

  ค. A     Z     %    ( )   ^

  ง. +    %    ( )   ^

8. นิพจน์ AB+  เรียกว่านิพจน์อะไร

  ก. นิพจน์อินฟิกซ์

  ข. นิพจน์โพสต์ฟิกซ์

  ค. นิพจน์พรีฟิกซ์

  ง. ไม่มีข้อใดถูก

9. แปลงนิพจน์ A+B/C*D=E

  ก. ABC/D*+E-

  ข. ABC/D*E+ -

  ค. ABC/D+E* -

  ง. ABC/D*E+ -

10. แปลงนิพจน์พรีฟิกซ์ - 5 + 9 * 3 – 1 2 เป็นนิพจน์โพสต์ฟิกซ์ได้คำตอบตามข้อใด

  ก. 5    9     3    1     2     -      *     +     -

  ข. 5  -  9   +   3   *   1   -   2

  ค. 5   9   -  3   *  1   +   2    

  ง. -    +     *    -   5     9      3      1      2

เฉลย 1.ก 2.ค 3.ข 4.ก 5.ก 6.ค 7.ข 8.ข 9.ก 10.ก